In this part of the activity, we are to familiarize how the FT works. We apply the FFT algorithm to images. We also the effect of fftshift() in the FT of the image and the results of double FFT.



Figure 1. (middle)Fourier transform and (right) double Fourier transform of the (left)image.
In 3D space, the circle (left) can be imagined as a cylinder. It can further be imagined as rectangles rotated about its center. A rectangular signal has a sinc transform. Now, a sinc rotated at its center produces an airy disk as observed in Fig.1 (middle). Also, the diameter of the center of the airy disk is small which is the inverse of the diameter of the circle which is a property of FT - changing to inverse space.
Fftshift() was already used on Fig.1(middle). Without using fftshift(), the FT looks like below:
Fftshift() was already used on Fig.1(middle). Without using fftshift(), the FT looks like below:


Figure 2. FT (left)with and (wihtout) using fftshift
As observed, the center of the airy disc are separated to the four corners of the image. This is an effect of the FT. The diagonal quadrants of the FT are interchanged. fftshift() interchanges the quadrants back resulting to Fig. 1(right).
Using a different image, as in Fig. 3(left), images alongside with it were obtained.
Using a different image, as in Fig. 3(left), images alongside with it were obtained.



Figure 3. (middle) FT and (right) double FT of the (left) image.
Notice that Fig.3(right) is an inverted image of Fig.3(left). The same happened in Fig.1 - although not obvious since a circle is symmetric.
This should be expected since:
This should be expected since:
F{F{f(x)}} = f(-x)
leading to an inversion of the image.
Activity 5.B - Simulation of an Imaging Device





Figure 5. Images formed using different sizes of circular apertures.
In this part of the activity, images formed in an imaging system were simulated. Particularly, we have an object f (Fig.4) and an aperture g in Fig.5(upper) and simulate how image produced looks like using Convolution theorem. The algorithm is that the FT of f and g are multiplied and then inverse FT is done. This results to an image that looks like f and g. This is the image formed by g.






Figure 5. Images formed using different sizes of circular apertures.
It can be observed from the figure that the readability of the image decreases (the image becomes blurry).
Activity 5C. Template matching using correlation


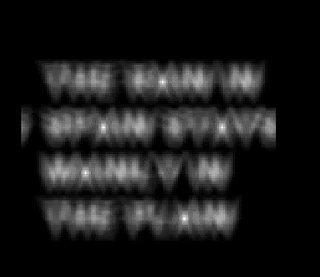
Figure 6. (left) the text used; (middle) the letter to be detected and (right) the image as a result of correlation
Correlation is a measure of how the a certain function is similar to another function, how similar an image to another image when talking about 2D arrays. One of its application is in pattern detection. Correlation values of highly similar functions is high as well. In this activity, we were tasked to find the letter A's contained in a text "The rain in Spain stays mainly in the plain."
Correlation is done using the equation below:
Correlation is done using the equation below:
p = f⊙g = f(-x,-y)* g(x,y)
where (*) represents the complex conjugate of the function.


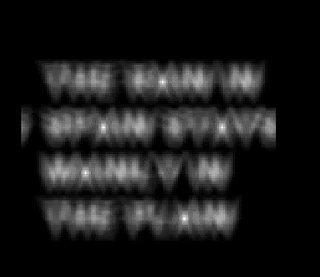
Figure 6. (left) the text used; (middle) the letter to be detected and (right) the image as a result of correlation
Upon applying correlation, Fig.6(right) was obtained. Bright spots on the image are high correlation values indicating an "A" pattern.
Activity 5D. Edge detection using convolution integral
In this part, using the image in Fig.4, we again exploit convolution to detect edges in the image. The idea is to convolve a desired pattern to find with the image being edge-detected. In other words, we find the certain pattern on the image.
Figure 7. Images upon application of edge-detection using (upper left) horizontal pattern; (upper right) vertical pattern; (lower left) diagonal pattern; and (lower right) a point.
We can see from the images that image detection algorithm allowed us to detect patterns on the image teh same as the desired pattern used(i.e, horizontal lines appear on Fig.7(upper right) since the image was convolved with a horizontal pattern). it is also interesting to note that using a point pattern allows us to detect all edges of the image.
In this activity I give myself a grade of 10 for doing the activity right. =)
In this activity I give myself a grade of 10 for doing the activity right. =)






No comments:
Post a Comment