Activity 17 - Photometric Stereo

Objects appear different depending on where the light source illuminating it is located. Shadows form at different locations. In this activity, we demonstrate a shadow model and extract shape from the shadows. Models depend on the type light source (point source, line source, etc.) used and where the light source is located. One of the more simple model is when the light source is placed at infinity. In general, when the light source is nearby, the brightness of an object illuminated by it is given by:

B(P) = [ρ(P)n(P)•S(P)]/R(P)²

where B(P) is the brightness of the object, S(P) is a vector from the light source and R(P) is the distance of the light source from the object.
In an infinite light source, 1/r dependence of B(P) disappears and the vector S(P) becomes constant for every point in the object. Thus the equation becomes:

B(P) = ρ(P)n(P)•S_o

In capturing an image of an object, we assume that it is proportional to the brightness of the object:

I(x,y) = kB(x,y) = kρ(x,y)n(x,y)•S_o = g(x,y)•V_o

where g(x,y) = ρ(x,y)n(x,y) and V_o=kS_o.

When an object is illuminated by light N light sources, Vo takes the form:

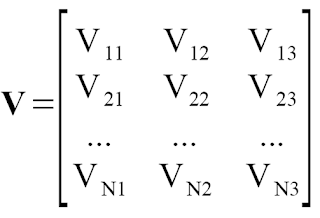
Each row represents the position (x,y,z) of the source in 3D space. Given an image with its intensity equal to its grayscale value, we can determine g(x,y) using the equation above. If we took a N captures of the surface of object illuminated by N light sources, then for each point (x,y):

I₁(x,y) = V₁₁g₁ + V₁₂g₂ + V₁₃g₃
I₂(x,y) = V₂₁g₁ + V₂₂g₂ + V₂₃g₃
I_N(x,y) = V_N1g₁ + V_N2g₂ + V_N3g₃

or in matrix form:

I = gV

Since we know I and V, we can calculate g using:

g = (V^TV)^-1VI

The normal vector can be solved by:

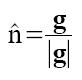
To get the surface elevation of point (u,v) on the surface, we use:

where

In this activity, we captured four images of a hemisphere illuminated by a far away light source located at four positions V:

(0.085832, 0.17365, 0.98106)
(0.085832, -0.17365, 0.98106)
(0.173650, 0.0, 0.98481)
(0.163180, -0.34202, 0.92542)

Below are the images taken for each light source locations.

Figure 1. Images of a hemispheres illuminated by a light source located at different positions

Using the procedure above, we obtained a 3D image of the surface shown in Fig.2.

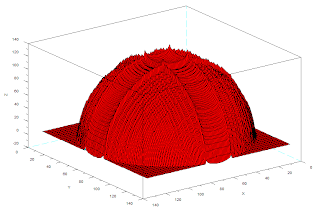
Figure 2. 3D reconstruction of the hemisphere

Here, we have successfully reconstructed the image. The reconstruction, however, is not smooth. Some parts do not follow the contour of a hemisphere.

In this activity, I give myself a grade of 10 for a successful reconstruction of the surface.

I thank Irene, Alva, Orly for very very useful help. :)